TESS Atlas fit for TOI 3114#

Version: ‘0.2.1.dev314+ge1761e8’

Note: This notebook was automatically generated as part of the TESS Atlas project. More information can be found on GitHub: github.com/dfm/tess-atlas

In this notebook, we do a quicklook fit for the parameters of the TESS Objects of Interest (TOI) in the system number 3114. To do this fit, we use the exoplanet library and you can find more information about that project at exoplanet.dfm.io.

From here, you can

scroll down and take a look at the fit results
open the notebook in Google Colab to run the fit yourself
download the notebook

Caveats#

There are many caveats associated with this relatively simple “quicklook” type of analysis that should be kept in mind. Here are some of the main things that come to mind:

The orbits that we fit are constrained to be circular. One major effect of this approximation is that the fit will significantly overestimate the confidence of the impact parameter constraint, so the results for impact parameter shouldn’t be taken too seriously.
Transit timing variations, correlated noise, and (probably) your favorite systematics are ignored. Sorry!
This notebook was generated automatically without human intervention. Use at your own risk!

Getting started#

To get going, we’ll add some magic, import some packages, and run some setup steps.

Downloading Data#

Next, we grab some inital guesses for the TOI’s parameters from ExoFOP and download the TOI’s lightcurve with Lightkurve.

We wrap the information in three objects, a TIC Entry, a Planet Candidate and finally a Lightcurve Data object.

The TIC Entry object holds one or more Planet Candidates (each candidate associated with one TOI id number) and a Lightcurve Data for associated with the candidates. Note that the Lightcurve Data object is initially the same fopr each candidate but may be masked according to the candidate transit’s period.
The Planet Candidate holds information on the TOI data collected by SPOC (eg transit period, etc)
The Lightcurve Data holds the lightcurve time and flux data for the planet candidates.

Downloading the data (this may take a few minutes):

tic_entry = TICEntry.load(toi=TOI_NUMBER)
tic_entry

time: 620 ms (started: 2023-08-11 14:16:36 +10:00)

TOI	3114.01
TOI	3114.01
Classification	Planet Candidate
Period (days)	4.407111
Epoch (TBJD)	2331.60796
Depth (ppt)	9.14
Duration (days)	0.088917
Planet SNR	61.0
Single Transit	False
PE Pipeline	QLP
Comments	found in faint-star QLP search

More data on ExoFOP page

If the amount of lightcurve data availible is large we filter the data to keep only data around transits.

if tic_entry.lightcurve.len > 1e5:
    tic_entry.lightcurve.filter_non_transit_data(tic_entry.candidates)
else:
    logger.info("Using the full lightcurve for analysis.")

time: 1.08 ms (started: 2023-08-11 14:16:36 +10:00)

Plot of the lightcurve:

plot_lightcurve(tic_entry, save=True)

# Some diagnostics
plot_raw_lightcurve(tic_entry, save=True)
plot_raw_lightcurve(tic_entry, zoom_in=True, save=True)

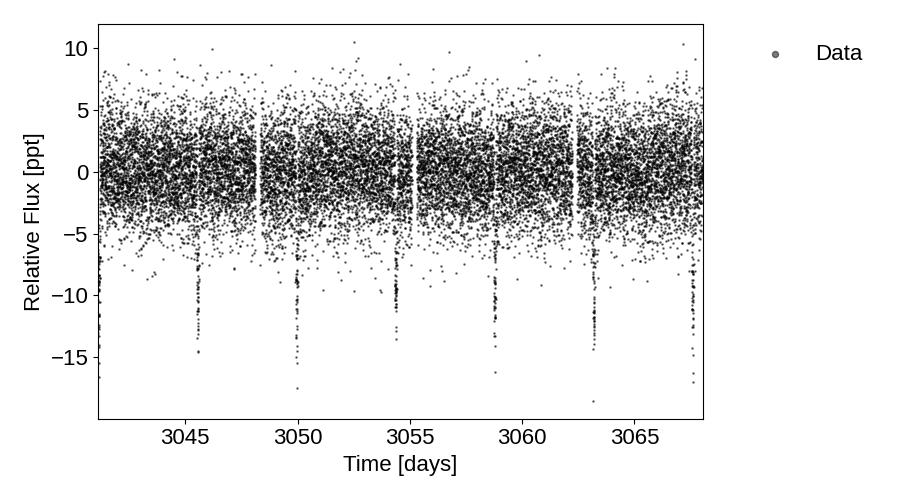
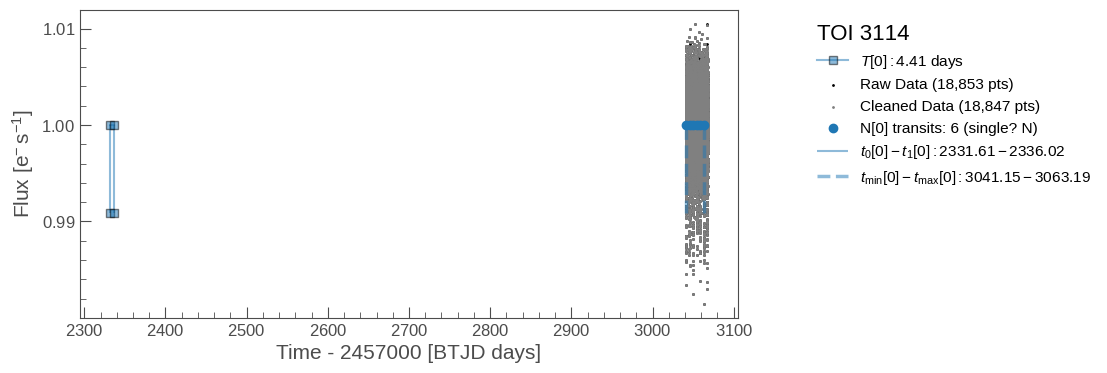
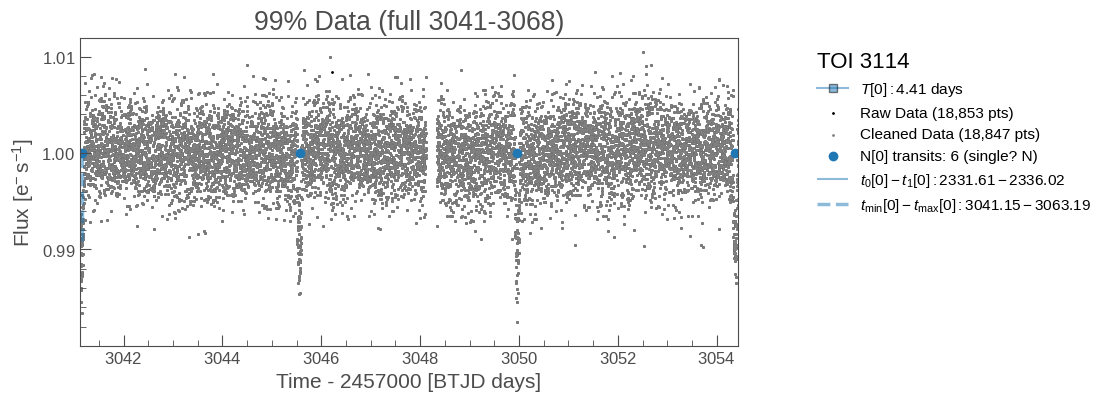
Diagnostic plots of the raw lightcurve (not applying sigma clipping/other cleaning methods to remove outliers). Some things to consider:

Do the initial fits from ExoFOP match the transits if visible?
If this is marked as a single-transit event, is there only 1 transit visible?

Fitting transit parameters#

Now that we have the data, we can define a Bayesian model to fit it.

The probabilistic model#

We use the probabilistic model as described in Foreman-Mackey et al 2017 to determine the best parameters to fit the transits present in the lightcurve data.

More explicitly, the stellar light curve $l(t; \vec{\theta})$ is modelled with a Gaussian Process (GP). A GP consists of a mean function $\mu(t;\vec{\theta})$ and a kernel function $k_\alpha(t,t’;\vec{\theta})$, where $\vec{\theta}$ is the vector of parameters descibing the lightcurve and $t$ is the time during which the lightcurve is under observation

The 8 parameters describing the lightcurve are $$\vec{\theta} = {d_i, t0_i, tmax_i, b_i, r_i, f0, u1, u2},$$ where

$d_i$ transit durations for each planet,
$tmin_i$ time of first transit for each planet (reference time),
$tmax_i$ time of the last transit for each planet (a second reference time),
$b_i$ impact parameter for each planet,
$r_i$ planet radius in stellar radius for each planet,
$f0$ baseline relative flux of the light curve from star,
$u1$ $u2$ two parameters describing the limb-darkening profile of star.

Note: if the observed data only records a single transit, we swap $tmax_i$ with $p_i$ (orbital periods for each planet).

With this we can write $$l(t;\vec{\theta}) \sim \mathcal{GP} (\mu(t;\vec{\theta}), k_\alpha(t,t’;\vec{\theta}))\ .$$

Here the mean and kernel functions are:

$\mu(t;\vec{\theta})$: a limb-darkened transit light curve (Kipping 2013)
$k_\alpha(t,t’;\vec{\theta}))$: a stochastically-driven, damped harmonic oscillator (SHOTterm)

Now that we have defined our transit model, we can implement it in python (toggle to show).

Show code cell content Hide code cell content

import aesara_theano_fallback.tensor as tt
import exoplanet as xo
import numpy as np
import pymc3 as pm
import pymc3_ext as pmx
from celerite2.theano import GaussianProcess, terms

DEPTH = "depth"
DURATION = "dur"
RADIUS_RATIO = "r"
TIME_START = "tmin"
TIME_END = "tmax"
ORBITAL_PERIOD = "p"
MEAN_FLUX = "f0"
LC_JITTER = "jitter"
GP_RHO = "rho"
GP_SIGMA = "sigma"
RHO_CIRC = "rho_circ"  # stellar density at e=0
LIMB_DARKENING_PARAM = "u"
IMPACT_PARAM = "b"


def get_test_duration(min_durations, max_durations, durations):
    largest_min_duration = np.amax(
        np.array([durations, 2 * min_durations]), axis=0
    )
    smallest_max_duration = np.amin(
        np.array([largest_min_duration, 0.99 * max_durations]), axis=0
    )
    return smallest_max_duration


def build_planet_transit_model(tic_entry):
    t = tic_entry.lightcurve.time
    y = tic_entry.lightcurve.flux
    yerr = tic_entry.lightcurve.flux_err

    n = tic_entry.planet_count
    tmins = np.array([planet.tmin for planet in tic_entry.candidates])
    depths = np.array([planet.depth for planet in tic_entry.candidates])
    durations = np.array([planet.duration for planet in tic_entry.candidates])
    max_durations = np.array(
        [planet.duration_max for planet in tic_entry.candidates]
    )
    min_durations = np.array(
        [planet.duration_min for planet in tic_entry.candidates]
    )
    test_duration = get_test_duration(min_durations, max_durations, durations)

    with pm.Model() as my_planet_transit_model:
        ## define planet parameters

        # 1) d: transit duration (duration of eclipse)
        d_priors = pm.Bound(
            pm.Lognormal, lower=min_durations, upper=max_durations
        )(
            name=DURATION,
            mu=np.log(durations),
            sigma=np.log(1.2),
            shape=n,
            testval=test_duration,
        )

        # 2) r: radius ratio (planet radius / star radius)
        r_priors = pm.Lognormal(
            name=RADIUS_RATIO, mu=0.5 * np.log(depths * 1e-3), sd=1.0, shape=n
        )
        # 3) b: impact parameter
        b_priors = xo.distributions.ImpactParameter(
            name=IMPACT_PARAM, ror=r_priors, shape=n
        )
        planet_priors = [r_priors, d_priors, b_priors]

        ## define orbit-timing parameters

        # 1) tmin: the time of the first transit in data (a reference time)
        tmin_norm = pm.Bound(
            pm.Normal, lower=tmins - max_durations, upper=tmins + max_durations
        )
        tmin_priors = tmin_norm(
            TIME_START, mu=tmins, sigma=0.5 * durations, shape=n, testval=tmins
        )

        # 2) period: the planets' orbital period
        p_params, p_priors_list, tmax_priors_list = [], [], []
        for n, planet in enumerate(tic_entry.candidates):
            # if only one transit in data we use the period
            if planet.has_data_only_for_single_transit:
                p_prior = pm.Pareto(
                    name=f"{ORBITAL_PERIOD}_{planet.index}",
                    m=planet.period_min,
                    alpha=2.0 / 3.0,
                    testval=planet.period,
                )
                p_param = p_prior
                tmax_prior = planet.tmin
            # if more than one transit in data we use a second time reference (tmax)
            else:
                tmax_norm = pm.Bound(
                    pm.Normal,
                    lower=planet.tmax - planet.duration_max,
                    upper=planet.tmax + planet.duration_max,
                )
                tmax_prior = tmax_norm(
                    name=f"{TIME_END}_{planet.index}",
                    mu=planet.tmax,
                    sigma=0.5 * planet.duration,
                    testval=planet.tmax,
                )
                p_prior = (tmax_prior - tmin_priors[n]) / planet.num_periods
                p_param = tmax_prior

            p_params.append(p_param)  # the param needed to calculate p
            p_priors_list.append(p_prior)
            tmax_priors_list.append(tmax_prior)

        p_priors = pm.Deterministic(ORBITAL_PERIOD, tt.stack(p_priors_list))
        tmax_priors = pm.Deterministic(TIME_END, tt.stack(tmax_priors_list))

        ## define stellar parameters

        # 1) f0: the mean flux from the star
        f0_prior = pm.Normal(name=MEAN_FLUX, mu=0.0, sd=10.0)

        # 2) u1, u2: limb darkening parameters
        u_prior = xo.distributions.QuadLimbDark("u")
        stellar_priors = [f0_prior, u_prior]

        ## define k(t, t1; parameters)
        jitter_prior = pm.InverseGamma(
            name=LC_JITTER, **pmx.estimate_inverse_gamma_parameters(1.0, 5.0)
        )
        sigma_prior = pm.InverseGamma(
            name=GP_SIGMA, **pmx.estimate_inverse_gamma_parameters(1.0, 5.0)
        )
        rho_prior = pm.InverseGamma(
            name=GP_RHO, **pmx.estimate_inverse_gamma_parameters(0.5, 10.0)
        )
        kernel = terms.SHOTerm(sigma=sigma_prior, rho=rho_prior, Q=0.3)
        noise_priors = [jitter_prior, sigma_prior, rho_prior]

        ## define the lightcurve model mu(t;paramters)
        orbit = xo.orbits.KeplerianOrbit(
            period=p_priors,
            t0=tmin_priors,
            b=b_priors,
            duration=d_priors,
            ror=r_priors,
        )
        star = xo.LimbDarkLightCurve(u_prior)
        lightcurve_models = star.get_light_curve(orbit=orbit, r=r_priors, t=t)
        lightcurve = 1e3 * pm.math.sum(lightcurve_models, axis=-1) + f0_prior
        my_planet_transit_model.lightcurve_models = lightcurve_models
        rho_circ = pm.Deterministic(name=RHO_CIRC, var=orbit.rho_star)

        # Finally the GP likelihood
        residual = y - lightcurve
        gp_kwargs = dict(diag=yerr**2 + jitter_prior**2, quiet=True)
        gp = GaussianProcess(kernel, t, **gp_kwargs)
        gp.marginal(name="obs", observed=residual)
        my_planet_transit_model.gp_mu = gp.predict(residual, return_var=False)

        # cache params
        my_params = dict(
            planet_params=planet_priors,
            noise_params=noise_priors,
            stellar_params=stellar_priors,
            period_params=p_params,
        )
    return my_planet_transit_model, my_params

time: 39.9 ms (started: 2023-08-11 14:16:38 +10:00)

planet_transit_model, params = build_planet_transit_model(tic_entry)
model_varnames = get_untransformed_varnames(planet_transit_model)
test_model(planet_transit_model)

time: 3min 27s (started: 2023-08-11 14:16:39 +10:00)

Optimizing the initial point for sampling#

We help out the sampler we try to find an optimized set of initial parameters to begin sampling from.

if tic_entry.optimized_params is None:
    init_params = get_optimized_init_params(planet_transit_model, **params)
    tic_entry.save_data(optimized_params=init_params)
else:
    init_params = tic_entry.optimized_params.to_dict()

# sanity check that none of the right hand column have nans!
test_model(planet_transit_model, init_params, show_summary=True)

time: 2.04 s (started: 2023-08-11 14:20:07 +10:00)

	Test Point	log P(test-point)
dur_interval__	-2.229	0.25
r_log__	-2.348	-0.92
b_impact__	-0.175	-1.56
tmin_interval__	0.0	1.38
tmax_1_interval__	0.0	1.38
f0	0.0	-3.22
u_quadlimbdark__	0.0	-2.78
jitter_log__	0.556	-19.94
sigma_log__	0.556	-6.06
rho_log__	0.053	-1.99
obs	NaN	-45804.69

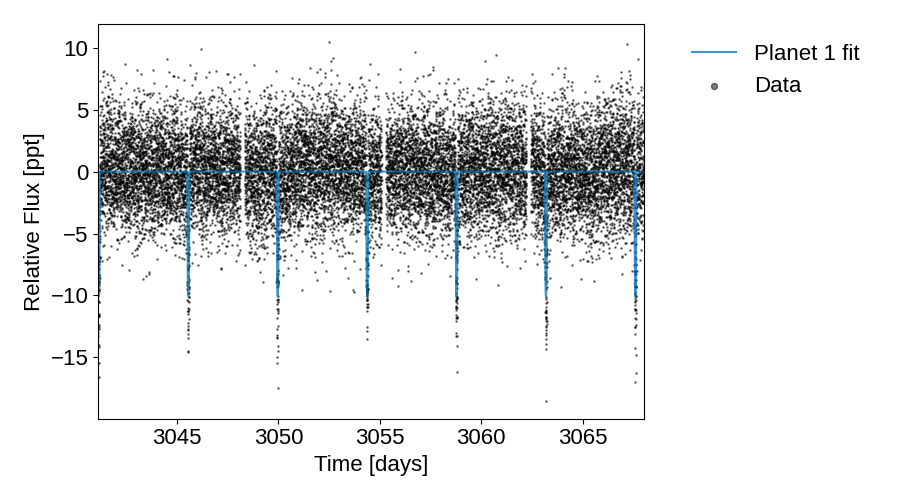
Below are plots of our initial model and priors.

Initial model fit#

initial_lc_models = (
    compute_variable(
        model=planet_transit_model,
        samples=[[init_params[n] for n in model_varnames]],
        target=planet_transit_model.lightcurve_models,
    )
    * 1e3
)
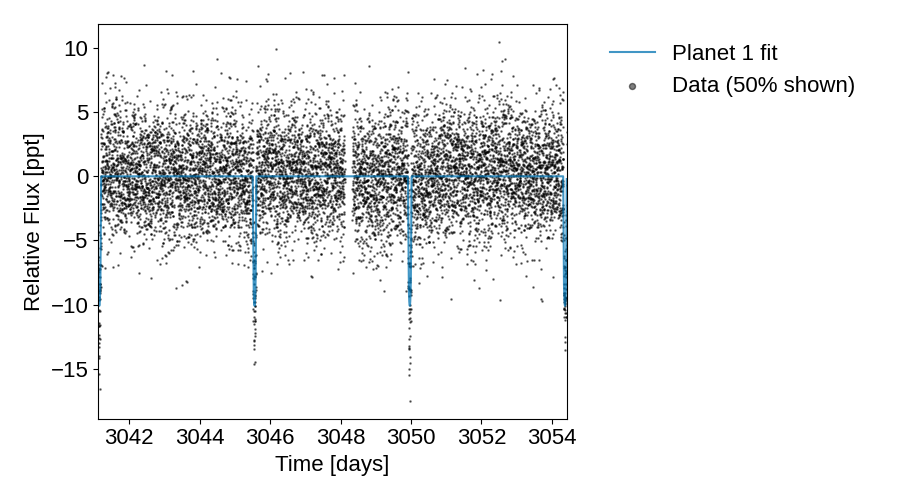
plot_lightcurve(
    tic_entry, initial_lc_models, save="lightcurve_with_initial_guess.png"
)
plot_lightcurve(
    tic_entry,
    initial_lc_models,
    zoom_in=True,
    save="lightcurve_with_initial_guess_zoom.png",
)

params = dict(
    tic_entry=tic_entry, model=planet_transit_model, initial_params=init_params
)
plot_phase(**params, save="phase_initial.png")
plot_phase(
    **params, plot_all_datapoints=True, save="phase_initial_all_datapoints.png"
)

Diagnostic phase plot

Histograms of Priors#

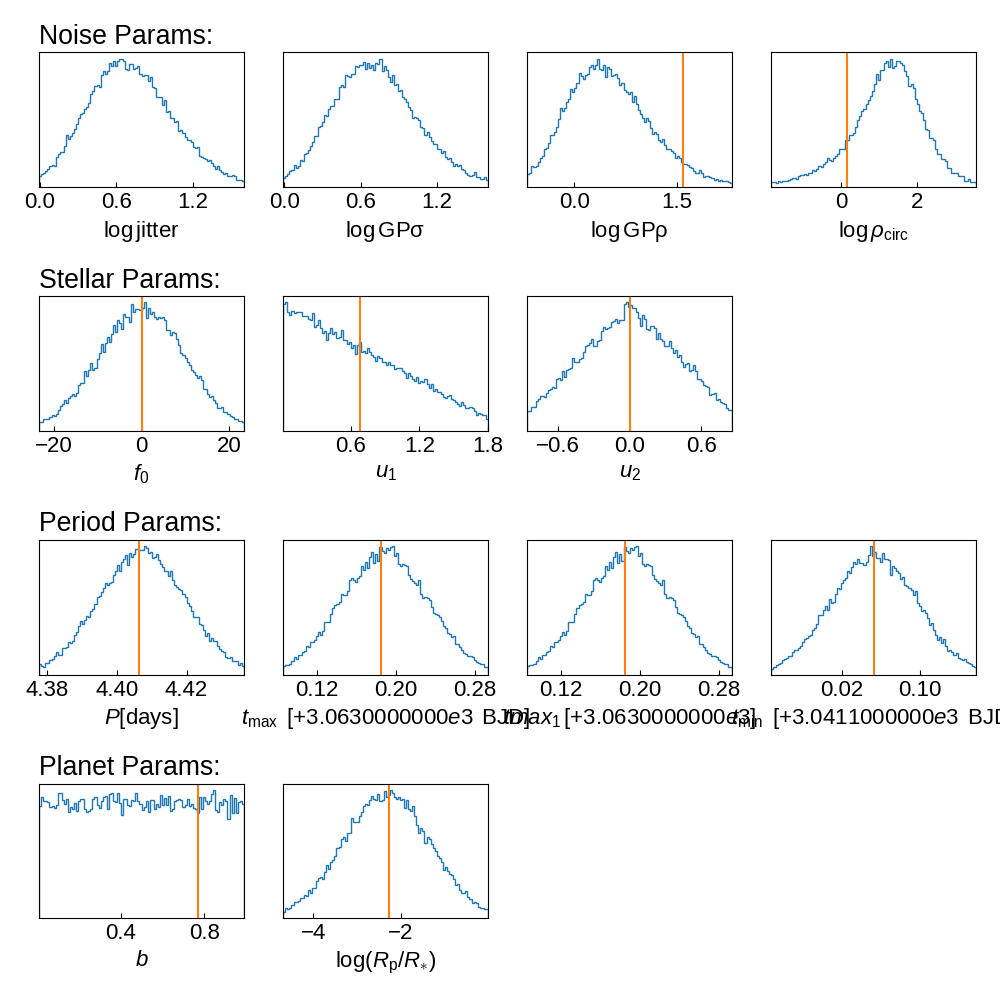
prior_samples = sample_prior(planet_transit_model)
if prior_samples:
    plot_priors(tic_entry, prior_samples, init_params, save=True)

Sampling#

With the model and priors defined, we can begin sampling.

def run_inference(model) -> InferenceData:
    np.random.seed(TOI_NUMBER)
    with model:
        sampling_kwargs = dict(tune=2000, draws=2000, chains=2, cores=2)
        logger.info(f"Run sampler with kwargs: {sampling_kwargs}")
        inference_data = pmx.sample(
            **sampling_kwargs, start=init_params, return_inferencedata=True
        )
        logger.info("Sampling completed!")
        return inference_data

time: 1.13 ms (started: 2023-08-11 14:20:25 +10:00)

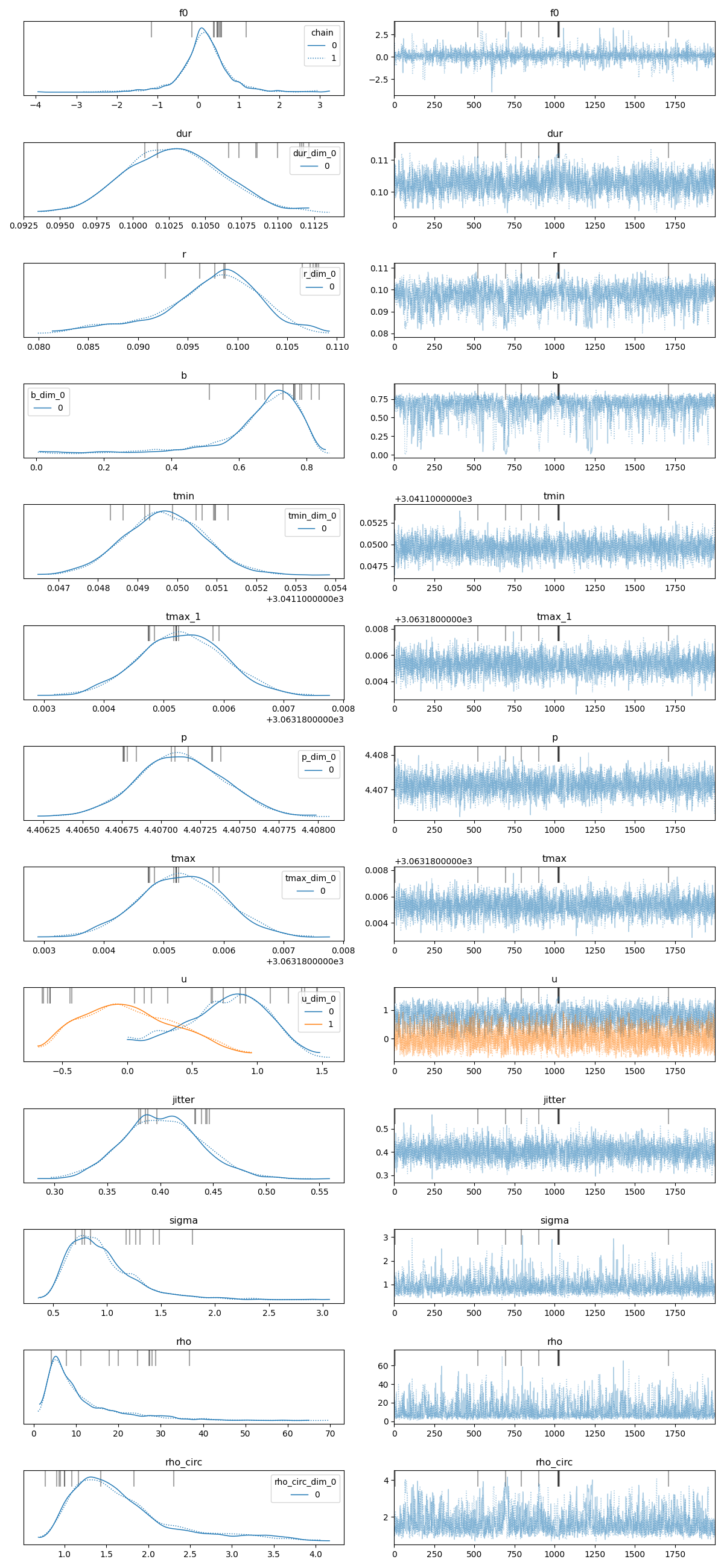
The inference_data object contains the posteriors and sampling metadata. Let’s save it for future use, and take a look at summary statistics. Note: the trace plot from sampling is hidden below.

summary(inference_data)

time: 216 ms (started: 2023-08-11 14:20:26 +10:00)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
f0	0.147	0.615	-1.040	1.357	0.019	0.014	1328.0	986.0	1.0
dur[0]	0.103	0.003	0.097	0.109	0.000	0.000	1083.0	942.0	1.0
r[0]	0.097	0.005	0.086	0.106	0.000	0.000	672.0	523.0	1.0
b[0]	0.653	0.148	0.347	0.832	0.007	0.005	704.0	424.0	1.0
tmin[0]	3041.150	0.001	3041.148	3041.152	0.000	0.000	2405.0	2350.0	1.0
tmax_1	3063.185	0.001	3063.184	3063.187	0.000	0.000	3122.0	2597.0	1.0
p[0]	4.407	0.000	4.407	4.408	0.000	0.000	2622.0	2344.0	1.0
tmax[0]	3063.185	0.001	3063.184	3063.187	0.000	0.000	3122.0	2597.0	1.0
u[0]	0.742	0.327	0.018	1.216	0.008	0.006	1515.0	1498.0	1.0
u[1]	0.031	0.366	-0.590	0.690	0.009	0.007	1745.0	1249.0	1.0
jitter	0.402	0.037	0.331	0.470	0.001	0.000	3378.0	2253.0	1.0
sigma	0.953	0.329	0.477	1.573	0.009	0.007	1683.0	1456.0	1.0
rho	11.177	8.850	1.634	28.897	0.249	0.176	1701.0	1954.0	1.0
rho_circ[0]	1.694	0.629	0.802	3.028	0.027	0.021	715.0	452.0	1.0

plot_inference_trace(tic_entry, save=True)

Results#

Posterior plots#

Below are plots of the posterior probability distributions and the best-fitting light-curve model.

plot_posteriors(
    tic_entry, inference_data, initial_params=init_params, save=True
)

%%memit
plot_phase(
    tic_entry,
    planet_transit_model,
    inference_data,
    initial_params=init_params,
    save=True,
)

Eccentricity post-processing#

As discussed above, we fit this model assuming a circular orbit which speeds things up for a few reasons:

e=0 allows simpler orbital dynamics which are more computationally efficient (no need to solve Kepler’s equation numerically)
There are degeneracies between eccentricity, arrgument of periasteron, impact parameter, and planet radius. Hence by setting e=0 and using the duration in calculating the planet’s orbit, the sampler can perform better.

To first order, the eccentricity mainly just changes the transit duration. This can be thought of as a change in the impled density of the star. Therefore, if the transit is fit using stellar density (or duration, in this case) as one of the parameters, it is possible to make an independent measurement of the stellar density, and in turn infer the eccentricity of the orbit as a post-processing step. The details of this eccentricity calculation method are described in Dawson & Johnson (2012).

Here, if the TIC has associated stellar data, we use the method described above to obtain fits for the exoplanet’s orbital eccentricity.

Note: a different stellar density parameter is required for each planet (if there is more than one planet)

star = tic_entry.stellar_data
star

time: 1.94 ms (started: 2023-08-11 14:20:45 +10:00)

Stellar Info:

mass = 0.96 ± 0.12 (Msun)
density = 0.58 ± 0.58 (solar)

time: 1.26 ms (started: 2023-08-11 14:20:45 +10:00)

if star.density_data_present:
    ecc_samples = calculate_eccentricity_weights(tic_entry, inference_data)
    ecc_samples.to_csv(
        os.path.join(tic_entry.outdir, "eccentricity_samples.csv"), index=False
    )
    plot_eccentricity_posteriors(tic_entry, ecc_samples, save=True)

Diagnostics#

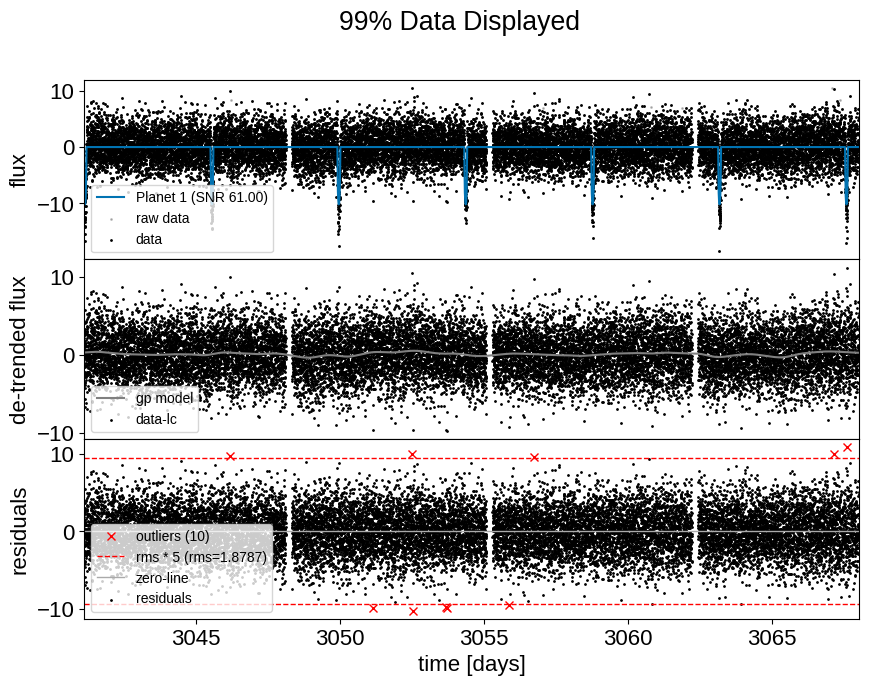
Finally, we also generate some diagnostic plots.

plot_diagnostics(tic_entry, planet_transit_model, init_params, save=True)

Citations#

We hope this has been helpful! The TESS-Atlas was built using exoplanet, PyMC3, lightkurve, starry, celerite2, ExoFOP, and Sphinx.

We would greatly appreciate you citing this work and its dependencies.

LaTeX acknowledgement and bibliography#

from tess_atlas import citations

citations.print_acknowledgements()

This research made use of the \textsf{TESS-Atlas} and its dependencies
\citep{exoplanet:joss, exoplanet:zenodo, celerite2:foremanmackey17,
celerite2:foremanmackey18, exoplanet:agol20, exoplanet:arviz,
exoplanet:astropy13, exoplanet:astropy18, exoplanet:kipping13,
exoplanet:luger18, exoplanet:pymc3, exoplanet:theano}.

time: 3.72 ms (started: 2023-08-11 14:20:54 +10:00)

citations.print_bibliography()

@article{exoplanet:joss,
       author = {{Foreman-Mackey}, Daniel and {Luger}, Rodrigo and {Agol}, Eric
                and {Barclay}, Thomas and {Bouma}, Luke G. and {Brandt},
                Timothy D. and {Czekala}, Ian and {David}, Trevor J. and
                {Dong}, Jiayin and {Gilbert}, Emily A. and {Gordon}, Tyler A.
                and {Hedges}, Christina and {Hey}, Daniel R. and {Morris},
                Brett M. and {Price-Whelan}, Adrian M. and {Savel}, Arjun B.},
        title = "{exoplanet: Gradient-based probabilistic inference for
                  exoplanet data \& other astronomical time series}",
      journal = {arXiv e-prints},
         year = 2021,
        month = may,
          eid = {arXiv:2105.01994},
        pages = {arXiv:2105.01994},
archivePrefix = {arXiv},
       eprint = {2105.01994},
 primaryClass = {astro-ph.IM},
       adsurl = {https://ui.adsabs.harvard.edu/abs/2021arXiv210501994F},
      adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}

@misc{exoplanet:zenodo,
  author = {Daniel Foreman-Mackey and Arjun Savel and Rodrigo Luger  and
            Eric Agol and Ian Czekala and Adrian Price-Whelan and
            Christina Hedges and Emily Gilbert and Luke Bouma
            and Timothy D. Brandt and Tom Barclay},
   title = {exoplanet-dev/exoplanet v0.5.1},
   month = jun,
    year = 2021,
     doi = {10.5281/zenodo.1998447},
     url = {https://doi.org/10.5281/zenodo.1998447}
}


@article{exoplanet:pymc3,
    title={Probabilistic programming in Python using PyMC3},
   author={Salvatier, John and Wiecki, Thomas V and Fonnesbeck, Christopher},
  journal={PeerJ Computer Science},
   volume={2},
    pages={e55},
     year={2016},
publisher={PeerJ Inc.}
}


@article{exoplanet:theano,
    title="{Theano: A {Python} framework for fast computation of mathematical
            expressions}",
   author={{Theano Development Team}},
  journal={arXiv e-prints},
   volume={abs/1605.02688},
     year=2016,
    month=may,
      url={http://arxiv.org/abs/1605.02688}
}


@article{exoplanet:arviz,
    title={{ArviZ} a unified library for exploratory analysis of {Bayesian}
           models in {Python}},
   author={Kumar, Ravin and Carroll, Colin and Hartikainen, Ari and Martin,
           Osvaldo A.},
  journal={The Journal of Open Source Software},
     year=2019,
      doi={10.21105/joss.01143},
      url={http://joss.theoj.org/papers/10.21105/joss.01143}
}


@ARTICLE{exoplanet:kipping13,
   author = {{Kipping}, D.~M.},
    title = "{Efficient, uninformative sampling of limb darkening coefficients
              for two-parameter laws}",
  journal = {\mnras},
     year = 2013,
    month = nov,
   volume = 435,
    pages = {2152-2160},
      doi = {10.1093/mnras/stt1435},
   adsurl = {http://adsabs.harvard.edu/abs/2013MNRAS.435.2152K},
  adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}


@article{exoplanet:astropy13,
   author = {{Astropy Collaboration} and {Robitaille}, T.~P. and {Tollerud},
             E.~J. and {Greenfield}, P. and {Droettboom}, M. and {Bray}, E. and
             {Aldcroft}, T. and {Davis}, M. and {Ginsburg}, A. and
             {Price-Whelan}, A.~M. and {Kerzendorf}, W.~E. and {Conley}, A. and
             {Crighton}, N. and {Barbary}, K. and {Muna}, D. and {Ferguson}, H.
             and {Grollier}, F. and {Parikh}, M.~M. and {Nair}, P.~H. and
             {Unther}, H.~M. and {Deil}, C. and {Woillez}, J. and {Conseil}, S.
             and {Kramer}, R. and {Turner}, J.~E.~H. and {Singer}, L. and
             {Fox}, R. and {Weaver}, B.~A. and {Zabalza}, V. and {Edwards},
             Z.~I. and {Azalee Bostroem}, K. and {Burke}, D.~J. and {Casey},
             A.~R. and {Crawford}, S.~M. and {Dencheva}, N. and {Ely}, J. and
             {Jenness}, T. and {Labrie}, K. and {Lim}, P.~L. and
             {Pierfederici}, F. and {Pontzen}, A. and {Ptak}, A. and {Refsdal},
             B. and {Servillat}, M. and {Streicher}, O.},
    title = "{Astropy: A community Python package for astronomy}",
  journal = {\aap},
     year = 2013,
    month = oct,
   volume = 558,
    pages = {A33},
      doi = {10.1051/0004-6361/201322068},
   adsurl = {http://adsabs.harvard.edu/abs/2013A%26A...558A..33A},
  adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}

@article{exoplanet:astropy18,
   author = {{Astropy Collaboration} and {Price-Whelan}, A.~M. and
             {Sip{\H o}cz}, B.~M. and {G{\"u}nther}, H.~M. and {Lim}, P.~L. and
             {Crawford}, S.~M. and {Conseil}, S. and {Shupe}, D.~L. and
             {Craig}, M.~W. and {Dencheva}, N. and {Ginsburg}, A. and
             {VanderPlas}, J.~T. and {Bradley}, L.~D. and
             {P{\'e}rez-Su{\'a}rez}, D. and {de Val-Borro}, M.
             and {Aldcroft}, T.~L. and {Cruz}, K.~L. and {Robitaille}, T.~P.
             and {Tollerud}, E.~J. and {Ardelean}, C. and {Babej}, T. and
             {Bach}, Y.~P. and {Bachetti}, M. and {Bakanov}, A.~V. and
             {Bamford}, S.~P. and {Barentsen}, G. and {Barmby}, P. and
             {Baumbach}, A. and {Berry}, K.~L.  and {Biscani}, F. and
             {Boquien}, M. and {Bostroem}, K.~A. and {Bouma}, L.~G. and
             {Brammer}, G.~B. and {Bray}, E.~M. and {Breytenbach}, H. and
             {Buddelmeijer}, H. and {Burke}, D.~J. and {Calderone}, G. and
             {Cano Rodr{\'{\i}}guez}, J.~L. and {Cara}, M. and {Cardoso},
             J.~V.~M. and {Cheedella}, S. and {Copin}, Y. and {Corrales}, L.
             and {Crichton}, D. and {D'Avella}, D. and {Deil}, C. and
             {Depagne}, {\'E}. and {Dietrich}, J.~P. and {Donath}, A. and
             {Droettboom}, M. and {Earl}, N. and {Erben}, T. and {Fabbro}, S.
             and {Ferreira}, L.~A. and {Finethy}, T. and {Fox}, R.~T. and
             {Garrison}, L.~H. and {Gibbons}, S.~L.~J. and {Goldstein}, D.~A.
             and {Gommers}, R. and {Greco}, J.~P. and {Greenfield}, P. and
             {Groener}, A.~M. and {Grollier}, F. and {Hagen}, A. and {Hirst},
             P. and {Homeier}, D. and {Horton}, A.~J. and {Hosseinzadeh}, G.
             and {Hu}, L. and {Hunkeler}, J.~S. and {Ivezi{\'c}}, {\v Z}. and
             {Jain}, A. and {Jenness}, T. and {Kanarek}, G. and {Kendrew}, S.
             and {Kern}, N.~S. and {Kerzendorf}, W.~E. and {Khvalko}, A. and
             {King}, J. and {Kirkby}, D. and {Kulkarni}, A.~M. and {Kumar}, A.
             and {Lee}, A.  and {Lenz}, D.  and {Littlefair}, S.~P. and {Ma},
             Z. and {Macleod}, D.~M. and {Mastropietro}, M. and {McCully}, C.
             and {Montagnac}, S. and {Morris}, B.~M. and {Mueller}, M. and
             {Mumford}, S.~J. and {Muna}, D. and {Murphy}, N.~A. and {Nelson},
             S. and {Nguyen}, G.~H. and {Ninan}, J.~P. and {N{\"o}the}, M. and
             {Ogaz}, S. and {Oh}, S. and {Parejko}, J.~K.  and {Parley}, N. and
             {Pascual}, S. and {Patil}, R. and {Patil}, A.~A.  and {Plunkett},
             A.~L. and {Prochaska}, J.~X. and {Rastogi}, T. and {Reddy Janga},
             V. and {Sabater}, J.  and {Sakurikar}, P. and {Seifert}, M. and
             {Sherbert}, L.~E. and {Sherwood-Taylor}, H. and {Shih}, A.~Y. and
             {Sick}, J. and {Silbiger}, M.~T. and {Singanamalla}, S. and
             {Singer}, L.~P. and {Sladen}, P.~H. and {Sooley}, K.~A. and
             {Sornarajah}, S. and {Streicher}, O. and {Teuben}, P. and
             {Thomas}, S.~W. and {Tremblay}, G.~R. and {Turner}, J.~E.~H. and
             {Terr{\'o}n}, V.  and {van Kerkwijk}, M.~H. and {de la Vega}, A.
             and {Watkins}, L.~L. and {Weaver}, B.~A. and {Whitmore}, J.~B. and
             {Woillez}, J.  and {Zabalza}, V. and {Astropy Contributors}},
    title = "{The Astropy Project: Building an Open-science Project and Status
              of the v2.0 Core Package}",
  journal = {\aj},
     year = 2018,
    month = sep,
   volume = 156,
    pages = {123},
      doi = {10.3847/1538-3881/aabc4f},
   adsurl = {http://adsabs.harvard.edu/abs/2018AJ....156..123A},
  adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}


@article{exoplanet:luger18,
   author = {{Luger}, R. and {Agol}, E. and {Foreman-Mackey}, D. and {Fleming},
             D.~P. and {Lustig-Yaeger}, J. and {Deitrick}, R.},
    title = "{starry: Analytic Occultation Light Curves}",
  journal = {\aj},
     year = 2019,
    month = feb,
   volume = 157,
    pages = {64},
      doi = {10.3847/1538-3881/aae8e5},
   adsurl = {http://adsabs.harvard.edu/abs/2019AJ....157...64L},
  adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}

@article{exoplanet:agol20,
   author = {{Agol}, Eric and {Luger}, Rodrigo and {Foreman-Mackey}, Daniel},
    title = "{Analytic Planetary Transit Light Curves and Derivatives for
              Stars with Polynomial Limb Darkening}",
  journal = {\aj},
     year = 2020,
    month = mar,
   volume = {159},
   number = {3},
    pages = {123},
      doi = {10.3847/1538-3881/ab4fee},
   adsurl = {https://ui.adsabs.harvard.edu/abs/2020AJ....159..123A},
  adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}


@article{exoplanet:foremanmackey17,
   author = {{Foreman-Mackey}, D. and {Agol}, E. and {Ambikasaran}, S. and
             {Angus}, R.},
    title = "{Fast and Scalable Gaussian Process Modeling with Applications to
              Astronomical Time Series}",
  journal = {\aj},
     year = 2017,
    month = dec,
   volume = 154,
    pages = {220},
      doi = {10.3847/1538-3881/aa9332},
   adsurl = {http://adsabs.harvard.edu/abs/2017AJ....154..220F},
  adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}
@article{exoplanet:foremanmackey18,
   author = {{Foreman-Mackey}, D.},
    title = "{Scalable Backpropagation for Gaussian Processes using Celerite}",
  journal = {Research Notes of the American Astronomical Society},
     year = 2018,
    month = feb,
   volume = 2,
   number = 1,
    pages = {31},
      doi = {10.3847/2515-5172/aaaf6c},
   adsurl = {http://adsabs.harvard.edu/abs/2018RNAAS...2a..31F},
  adsnote = {Provided by the SAO/NASA Astrophysics Data System}
}

time: 1.29 ms (started: 2023-08-11 14:20:54 +10:00)

Packages used#

citations.print_packages()

zipp==3.6.0
xarray==0.19.0
widgetsnbextension==3.5.1
wheel==0.37.0
websocket-client==1.2.1
webencodings==0.5.1
wcwidth==0.2.5
virtualenv==20.8.1
urllib3==1.26.7
uncertainties==3.1.6
uc-micro-py==1.0.1
typing-extensions==3.10.0.2
traitlets==5.1.0
tqdm==4.62.3
tornado==6.1
tomli==1.2.1
toml==0.10.2
tinycss2==1.2.1
threadpoolctl==3.0.0
Theano-PyMC==1.1.2
testpath==0.5.0
testbook==0.4.2
tess-atlas==0.2.1.dev314+ge1761e8
terminado==0.12.1
tenacity==8.0.1
tar-progress==1.3.3
tabulate==0.8.10
tables==3.7.0
StrEnum==0.4.15
SQLAlchemy==1.4.26
sphinxcontrib-serializinghtml==1.1.5
sphinxcontrib-qthelp==1.0.3
sphinxcontrib-jsmath==1.0.1
sphinxcontrib-htmlhelp==2.0.0
sphinxcontrib-devhelp==1.0.2
sphinxcontrib-bibtex==2.2.1
sphinxcontrib-applehelp==1.0.2
Sphinx==5.0.2
sphinx-toolbox==3.1.2
sphinx-togglebutton==0.2.2
sphinx-thebe==0.2.1
sphinx-tabs==1.2.1
sphinx-remove-toctrees==0.0.3
sphinx-prompt==1.5.0
sphinx-panels==0.6.0
sphinx-multitoc-numbering==0.1.3
sphinx-jupyterbook-latex==0.5.2
sphinx-jinja2-compat==0.1.2
sphinx-external-toc==0.3.1
sphinx-design==0.3.0
sphinx-copybutton==0.4.0
sphinx-comments==0.0.3
sphinx-collapse==0.1.2
sphinx-book-theme==1.0.1
sphinx-autodoc-typehints==1.18.3
soupsieve==2.2.1
snowballstemmer==2.1.0
sniffio==1.2.0
smmap==4.0.0
six==1.16.0
setuptools==47.1.0
Send2Trash==1.8.0
semver==2.13.0
SecretStorage==3.3.1
seaborn==0.11.2
scipy==1.7.1
scikit-learn==1.0
SciencePlots==1.0.9
ruamel.yaml==0.17.21
ruamel.yaml.clib==0.2.6
requests==2.26.0
requests-unixsocket==0.2.0
regex==2021.10.21
pyzmq==22.3.0
PyYAML==6.0
pyvo==1.1
pytz==2021.3
python-dateutil==2.8.2
pytest==7.4.0
pytest-cov==4.1.0
pyrsistent==0.18.0
pyparsing==2.4.7
Pympler==1.0.1
pymc3==3.11.4
pymc3-ext==0.1.0
Pygments==2.15.1
pyflakes==2.4.0
pyerfa==2.0.0
pydmove==1.1
pydata-sphinx-theme==0.13.3
pycparser==2.20
pycodestyle==2.8.0
pybtex==0.24.0
pybtex-docutils==1.0.1
py==1.10.0
ptyprocess==0.7.0
psutil==5.9.1
prompt-toolkit==3.0.20
prometheus-client==0.11.0
pretty-jupyter==2.0.5
posthog==3.0.1
pluggy==1.0.0
plotly==5.3.1
ploomber-engine==0.0.30
ploomber-core==0.2.12
platformdirs==2.4.0
pip==23.2.1
Pillow==8.4.0
pikepdf==5.1.3
pickleshare==0.7.5
pexpect==4.8.0
patsy==0.5.2
pathspec==0.9.0
parso==0.8.2
pandocfilters==1.5.0
pandas==1.3.4
packaging==21.0
opencv-python==4.6.0.66
oktopus==0.1.2
numpy==1.21.3
numexpr==2.8.3
notebook==6.4.5
nodeenv==1.6.0
netCDF4==1.5.7
nest-asyncio==1.5.1
nbformat==5.1.3
nbdime==3.1.0
nbconvert==6.5.4
nbclient==0.5.4
natsort==8.1.0
myst-parser==0.18.1
myst-nb==0.17.2
mypy-extensions==0.4.3
msgpack==1.0.4
monotonic==1.6
mock==4.0.3
mistune==0.8.4
mimeparse==0.1.3
memory-profiler==0.60.0
memoization==0.4.0
mdit-py-plugins==0.3.5
mccabe==0.6.1
matplotlib==3.4.3
matplotlib-inline==0.1.3
MarkupSafe==2.0.1
markdown-it-py==1.1.0
lxml==4.6.4
lockfile==0.12.2
linkify-it-py==2.0.2
lightkurve==2.0.11
latexcodec==2.0.1
kiwisolver==1.3.2
keyring==23.2.1
jupytext==1.11.5
jupyterlab-widgets==1.0.2
jupyterlab-pygments==0.2.2
jupyter-sphinx==0.3.2
jupyter-server==1.11.1
jupyter-server-mathjax==0.2.3
jupyter-resource-usage==0.6.1
jupyter-nbextensions-configurator==0.4.1
jupyter-latex-envs==1.4.6
jupyter-highlight-selected-word==0.2.0
jupyter-core==4.8.1
jupyter-contrib-nbextensions==0.5.1
jupyter-contrib-core==0.3.3
jupyter-client==6.1.12
jupyter-cache==0.6.1
jupyter-book==0.15.1
jsonschema==3.2.0
joblib==1.1.0
Jinja2==3.0.2
jeepney==0.7.1
jedi==0.18.0
itables==1.5.3
isort==5.9.3
ipywidgets==7.6.5
ipython==7.28.0
ipython-genutils==0.2.0
ipykernel==6.4.2
interruptingcow==0.8
iniconfig==1.1.1
importlib-resources==5.3.0
importlib-metadata==4.8.1
img2pdf==0.4.4
imagesize==1.4.1
idna==3.3
identify==2.3.0
html5lib==1.1
h5py==3.7.0
greenlet==1.1.2
GitPython==3.1.24
gitdb==4.0.7
future==0.18.2
flake8==4.0.1
filelock==3.3.1
fbpca==1.0
fastprogress==1.0.0
exoplanet==0.5.1
exoplanet-core==0.1.2
exceptiongroup==1.1.2
enum34==1.1.10
entrypoints==0.3
emcee==3.1.2
dynesty==1.0.1
domdf-python-tools==3.3.0
docutils==0.16
distlib==0.3.3
dill==0.3.4
dict2css==0.3.0
defusedxml==0.7.1
decorator==5.1.0
debugpy==1.5.1
debuglater==1.4.4
cycler==0.10.0
cssutils==2.5.0
cryptography==35.0.0
coverage==7.2.7
corner==2.2.1
colorama==0.4.4
click==7.1.2
charset-normalizer==2.0.7
cftime==1.5.1
cfgv==3.3.1
cffi==1.15.0
certifi==2021.10.8
Cerberus==1.3.4
celerite2==0.2.0
cachetools==4.2.4
CacheControl==0.12.11
pre-commit==2.15.0
bokeh==2.4.1
bleach==4.1.0
black==21.9b0
bilby==1.1.5
beautifulsoup4==4.10.0
backports.entry-points-selectable==1.1.0
backoff==2.2.1
backcall==0.2.0
Babel==2.9.1
autograd==1.3
autodocsumm==0.2.8
attrs==21.2.0
astroquery==0.4.3
astropy==4.3.1
arviz==0.11.4
argon2-cffi==21.1.0
apeye==1.2.0
anyio==3.3.4
alabaster==0.7.12
aesara-theano-fallback==0.0.4
accessible-pygments==0.0.4
ipython-autotime==0.3.1
jupyternotify==0.1.15
jupyter==1.0.0
qtconsole==5.3.1
jupyter-console==6.4.4
QtPy==2.1.0
time: 1.44 ms (started: 2023-08-11 14:20:54 +10:00)

TESS Atlas fit for TOI 3114

TESS Atlas